🔥 시간복잡도
🐛 시간복잡도 정의
알고리즘의 수행 시간을 분석할 때 시간 복잡도를 사용합니다.
🐛 기본 연산
데이터 입출력 - copy, move…
산술 연산 - add, multiply …
제어 연산 - if, while …
🐛 시간 복잡도의 3가지
- 최선의 경우 (Best Case)
- 빅 오메가 표기법 사용
- 최선의 시나리오로 최소 이만한 시간이 걸림
- 최악의 경우 (Worst Case)
- 빅 오 표기법 사용
- 최악의 시나리오로 아무리 오래 걸려도 이 시간보다 덜 걸림
- 평균적인 경우 (Average Case)
- 빅 세타 표기법 사용
- 평균 시간을 나타냄
평균적인 경우를 가장 많이 사용할 것 같지만 알고리즘이 복잡해질수록 평균적인 경우는 구하기가 매우 어려워 지기 때문에 최악의 경우로 알고리즘의 성능을 파악합니다.
🔥 시간복잡도 계산
🐛 빅오 표기법
1
2
3
4
5
6
7
8
9
10
11
12
func (n) {
let sum = 0; // 대입연산 1회
let ar i = 0; // 대입연산 1회
for(i=0; i < n; i++) { // 반복문 n+1회
sum += i; // 덧셈 연산 n회
}
for(i=0; i < n; i++) { // 반복문 n+1회
sum += i; // 덧셈 연산 n회
}
return sum; // 리턴 1회
}
위 알고리즘에 단계별 연산 횟수는 주석과 같고 총 연산 횟수는 4n+5입니다.
4n+5 = O(n)
🔥 시간복잡도 표기
🐛 O(1)-상수시간
1
2
3
func (n) {
console.log(n)
}
🐛 O(logN)-로그시간
입력 크기(N)가 커질 때 연산 횟수가 logN에 비례해서 증가하면 시간 복잡도는 O(logN)입니다.
1
2
3
for(i=0; i<n; i*n){
...
}
🐛 O(n)-선형시간
반복문
1
2
3
for(i=0; i<n; i++){
...
}
🐛 O(n^2)-2차시간
중첩 반복문
1
2
3
4
5
for(i=0; i<n; i++){
for(j=0; j<n; j++){
...
}
}
🐛 O(2^n)-지수시간
재귀
1
2
3
4
5
func (n) {
if (n <= 1)
return n;
return func(n-1) + func(n-2);
}
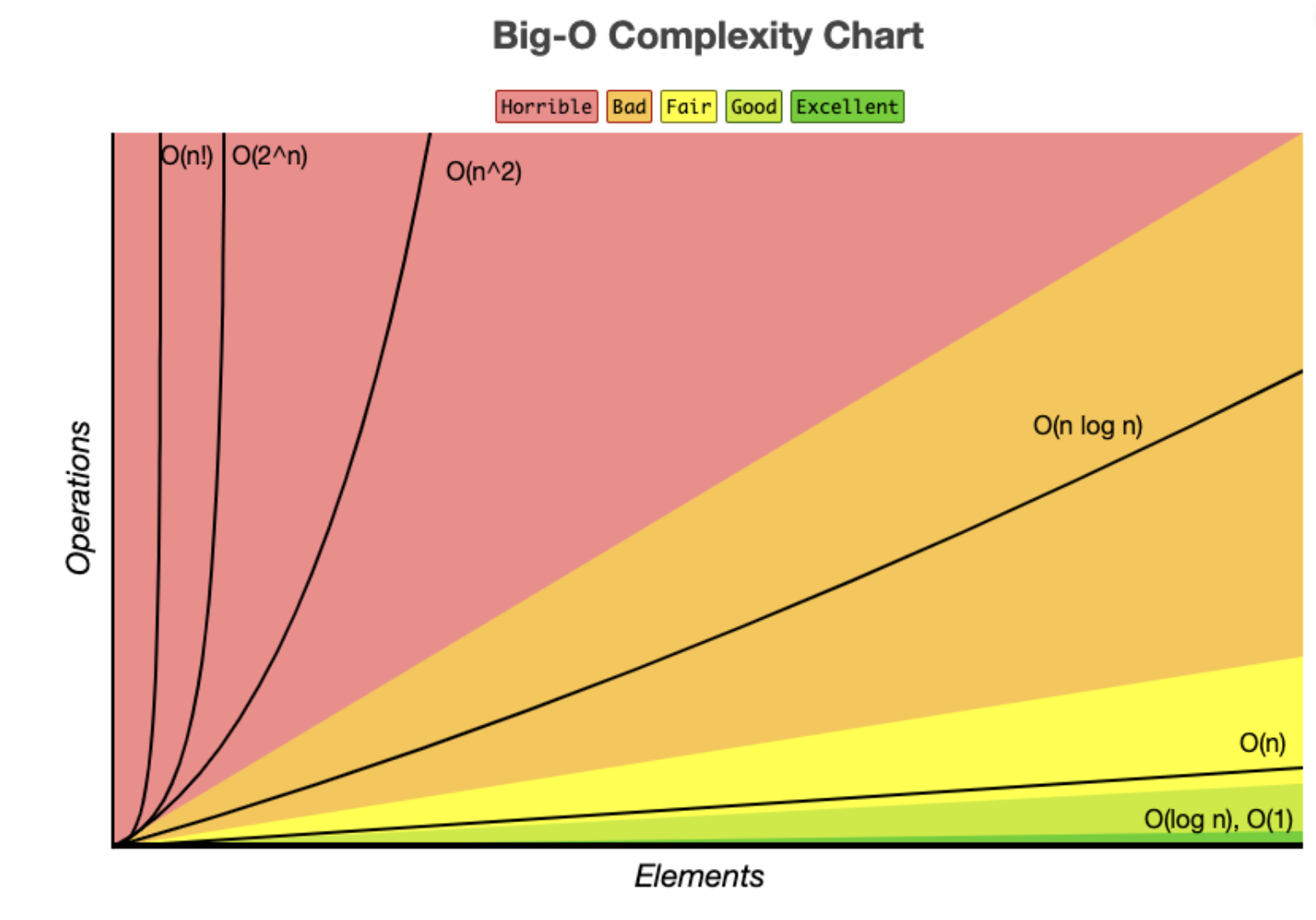
https://www.bigocheatsheet.com/
참고